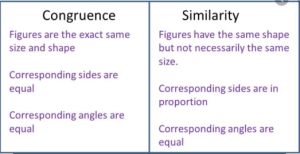
The Basic Difference between congruence and Similarity is that geometric figures are congruent if they have the same shape and dimension regardless of their orientation or position, in turn, they have similarities if they have the same shape regardless of the size they present.
What is mean By Congruence?
In mathematics, the congruence of two geometric figures is established when both have the same dimensions and the same shape regardless of their position or orientation. In other words, two figures are congruent if there is an isometry that relates them, a transformation that can be translation, rotation, and/or reflection.
The related parts between the congruent figures are known as homologous or corresponding.
After performing the isometry, when superimposing the figures, all the points must coincide.
For the figures to be congruent, they must meet the following requirements:
- All of your corresponding interior angles must be equal.
- All of its corresponding sides must have the same measurement.
In the case of triangles, the congruence of the 6 pairs of elements should not be checked (3 pairs of sides and 3 pairs of angles), under certain conditions, we can verify the congruence of three pairs of elements:
- Two triangles are congruent if their three sides are respectively equal.
- Two triangles are congruent, two of their sides are equal and the angle between them.
- Two triangles are congruent if they have a congruent side and the angles with a vertex at each end of that side are congruent.
- Two triangles are congruent if they have two congruent sides and the angles opposite the larger of the sides are also congruent.
What is Similarity in math?
In mathematics, two similar geometric figures are considered if they have the same shape regardless of their size.
The corresponding sides must be proportional based on a similarity ratio, scale factor, or constant of proportionality.
The similarity ratio is obtained when we divide the measure of one side by its corresponding, the number obtained must be constant for all sides of the figure.
For two figures to be similar, they must meet two conditions:
- Their corresponding (homologous) angles must be equal.
- Their corresponding sides are proportional.
In the case of triangles, the shape depends only on their angles, so the concept of similarity is simplified: Two triangles are similar if their angles are equal two to two.
To denote that two triangles ABC and DEF are similar, write ABC ~ DEF, the order indicates the correspondence that exists between the angles, that is, A, B and C correspond to D, E, and F, respectively.
Difference between congruence and similarity
In triangles, congruence occurs when two triangles are exactly equal, measure the same, and have the same angles regardless of their orientation.
Two geometric figures are congruent if they both have the same dimensions and the same shape regardless of their position or orientation.
The similarity in triangles occurs when these, despite not being identical, keep a proportion or scale on their sides and angles.
Two geometric figures are similar if they have the same shape regardless of their size.
This video will Explain Difference between similarity and Congruence
